Dreisatz: Einfach berechnen mit Beispielen + Formel

Was ist der Dreisatz?

Der Dreisatz zählt zu den wichtigsten mathematischen Lösungsverfahren. Dabei setzen Sie zwei bekannte Werte ins Verhältnis zueinander, um die gesuchte (unbekannte) Größe zu ermitteln. So berechnen Sie Proportionalaufgaben in drei Rechenschritten – daher die Bezeichnung.

Es gibt den proportionalen und den antiproportionalen Dreisatz. Beim proportionalen Dreisatz stehen zwei Werte proportional zueinander. Sinkt oder steigt Wert 1, sinkt oder steigt auch Wert 2. Andersherum beim antiproportionalen Dreisatz – sinkt der eine Wert, steigt der andere – und umgekehrt.

Proportionaler Dreisatz

Der proportionale Dreisatz funktioniert nach dem Prinzip: je mehr, desto mehr oder je weniger, desto weniger. Es liegt direkte Proportionalität zwischen Wert A und B vor. Simples Alltagsbeispiel: Je schneller Sie laufen, desto schneller sind Sie am Ziel. Oder: Je weniger Sie arbeiten, desto weniger Gehalt verdienen Sie.

Beispiel: Aufgabe zum proportionalen Dreisatz

Ein Sack mit 4 Kilo Kartoffeln kostet 8 Euro. Wie teuer sind 3 Kilogram der Kartoffeln? Über den Dreisatz berechnen Sie zunächst, was 1 Kilogramm kostet – und anschließend den Preis jeder beliebigen Menge. Die Rechnung geht folgendermaßen:

• 1. Schritt (Verhältnis)
  4 Kilogramm = 8 Euro
• 2. Schritt (beide Seiten geteilt durch 4)
  1 Kilogramm = 2 Euro
• 3. Schritt (beide Seiten multipliziert mit gesuchter Größe „3“)
  3 Kilogramm = 6 Euro

Rechnung mit Tabellenverfahren

Sie beginnen in einer zweispaltigen Tabelle und tragen in der ersten Zeile die bekannten Werte ein – im Beispiel die 4 (Kartoffeln/Kilogramm) und daneben die 8 (Preis/Euro). Für die Rechenschritte gehen Sie jeweils eine Zeile tiefer: Um im Zwischenschritt den Preis für ein Kilogramm zu berechnen, teilen Sie den Wert links durch 4 (also 4 : 4 = 1). Das Gleiche machen Sie mit dem Wert rechts (also 8 : 4 = 2)

Das Ergebnis erhalten Sie im dritten Schritt und multiplizieren beide Seiten mit der gesuchten Größe. Unten rechts in der Tabelle steht der gefragte Preis von 6 Euro für 3 Kilogram. Grafisch sieht das so aus:

Dreisatz Formel: Proportional

Die Formel für die Berechnung eines proportionalen Dreisatzes lautet:

(b / a) ∙ c = x

Sie teilen den Wert der bekannten Zuordnung (8 Euro) durch den anderen Wert (4 Kilogramm). Das Ergebnis multiplizieren Sie mit der gesuchten Menge (3 Kilogramm). Im obigen Beispiel lautet die Formel entsprechend: (8 / 4) ∙ 3 = 6

Antiproportionaler Dreisatz

Der antiproportionale Dreisatz (auch umgekehrter Dreisatz) funktioniert genau umgekehrt: je mehr, desto weniger. Man spricht von indirekter Proportionalität zwischen A und B. Auch hier Beispiele aus dem Alltag: Je mehr eine Person vom Kuchen isst, desto weniger bleibt übrig. Oder: Je mehr Menschen eine Aufgabe anpacken, desto geringer die Arbeitszeit.

Beispiel: Aufgabe zum antiproportionalen Dreisatz

5 Bagger benötigen insgesamt 12 Tage, um eine Baugrube zu füllen. Wie lange brauchen 8 Bagger, um dieselbe Baugrube zu füllen? Wichtigster Schritt ist es, die antiproportionale Zuordnung zu erkennen. Anschließend folgt die Rechnung:

• 1. Schritt (Verhältnis)
  5 Bagger = 12 Tage
• 2. Schritt (links geteilt durch 5, rechts multipliziert mit 5)
  1 Bagger = 60 Tage
• 3. Schritt (links multipliziert mit gesuchter Größe, rechts geteilt)
  8 Bagger = 7,5 Tage

Rechnung mit Tabellenverfahren

Sie tragen die bekannten Werte in die erste Zeile ein: 5 Bagger (links) und 12 Tage (rechts). In der zweiten Zeile berechnen Sie das Verhältnis für 1 Bagger – also geteilt durch 5. Weil dieser Dreisatz antiproportional ist, müssen Sie auf der rechten Seite mit 5 multiplizieren (= 60 Tage).

Für das Ergebnis mit 8 Baggern multiplizieren Sie die linke Seite mit 8, antiproportional teilen Sie die rechte Seite durch 8. So kommen Sie zu 7,5 Tage für 8 Bagger. Grafisch sieht das so aus:

Dreisatz Formel: Antiproportional

Die Formel für die Berechnung eines antiproportionalen Dreisatzes lautet:

(b ∙ a) / c = x

Sie multiplizieren den Wert der bekannten Zuordnung (12 Tage) mit dem anderen Wert (5 Bagger). Das Ergebnis teilen Sie durch die gesuchte Menge (8 Bagger). Im obigen Beispiel lautet die Formel: (12 ∙ 5) / 8 = 7,5.

Dreisatz Prozent

Eine häufige Aufgabe für den Dreisatz ist die Prozentrechnung. Dabei lassen sich sowohl Grundwerte als auch Prozentwerte ermitteln – abhängig von der Frage. Im Zwischenschritt ermitteln Sie entweder die Werte für 1 Prozent oder für 100 Prozent. Unser Beispiel zeigt, wie das funktioniert:

Beispiel: Aufgabe zum Dreisatz mit Prozenten

Eine Tafel Schokolade hat 2,50 Euro gekostet. Aufgrund geringer Haltbarkeit ist sie um 50 Prozent reduziert. Wie teuer ist die Schokolade jetzt? Wichtigste Erkenntnis: Die Schokolade kostet jetzt nur noch 50 Prozent des Ausgangswerts.

• 1. Schritt (Verhältnis)
  100 Prozent = 2,50 Euro
• 2. Schritt (beide Seiten geteilt durch 100)
  1 Prozent = 2,5 Cent
• 3. Schritt (beide Seiten multipliziert mit 50)
  50 Prozent = 1,25 Euro

Rechnung mit Tabellenverfahren

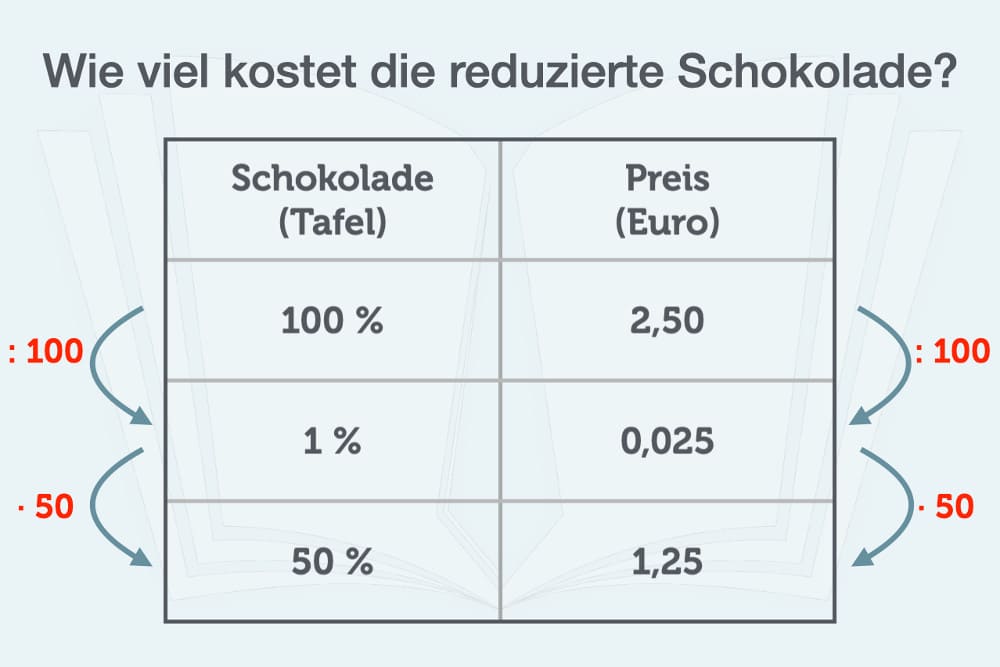
Der Dreisatz mit Prozenten in einer Tabelle funktioniert nach demselben Prinzip: In der ersten Zeile stehen die bekannten Werte: 100 Prozent (links) und 2,50 Euro (rechts). Für 1 Prozent teilen Sie durch 100 – da es ein proportionaler Dreisatz ist auf beiden Seiten (mehr Prozent = mehr Kosten).

In der dritten Zeile lösen Sie den Dreisatz durch Multiplikation auf beiden Seiten mit dem gesuchten Wert (50 Prozent). Die reduzierte Schokolade kostet 1,50 Euro. Grafisch sieht das so aus:

Prozentrechnung Formel

Die Formel zum Dreisatz für Prozente ändert sich nicht: Bei proportionalen Verhältnissen lautet sie (b / a) ∙ c = x, für antiproportionale ist es (b ∙ a) / c = x.

Im Beispiel rechnen Sie also (2,50 Euro / 100) ∙ 50 = 1,25 Euro

Übung: Dreisatz Aufgaben

Sind Sie bereit für den Dreisatz? Mit diesen Aufgaben und Übungen testen Sie Ihr Wissen. Die Antworten finden Sie jeweils im Anschluss:

1. Aufgabe: Gäste bewirten

Sie haben ein Spaghetti-Bolognese-Rezept für 4 Personen. Dafür benötigen Sie 600 Gramm Spaghetti. Wie viel mehr brauchen Sie, wenn sich eine fünfte Person dazugesellt?

Lösung: Proportionaler Dreisatz: (600 : 4) · 5 = 750 Gramm

2. Aufgabe: Küche montieren

Zwei Mitarbeiter eines Küchenstudios bauen eine Küche in 6 Stunden auf. Wie schnell würde es gehen, wenn sie noch einen dritten Kollegen hätten?

Lösung: Antiproportionaler Dreisatz: (6 · 2) : 3 = 4 Stunden

3. Aufgabe: Hose kaufen

Eine Hose hat 90 Euro gekostet. Im Schlussverkauf gibt es auf alle Hosen 30 Prozent Nachlass. Wie viel kostet die Hose nun?

Lösung: Prozent: (90 : 100) · 30 = 27 Euro Rabatt. Die Hose kostet 63 Euro.

4. Aufgabe: Rasen mähen

Zwei Gärtner mähen eine Parkanlage in 7 Stunden. Wie lange dauert es für 5 Gärtner?

Lösung: Antiproportionaler Dreisatz: (7 · 2) : 5 = 2,8 Stunden

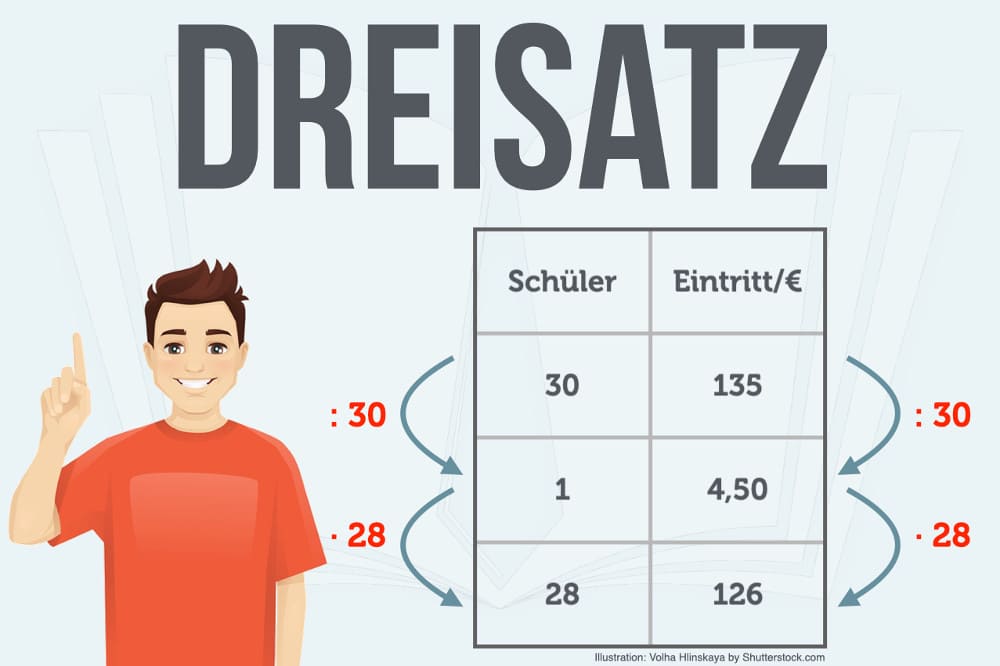
5. Aufgabe: Eintritt zahlen

Auf einem Klassenausflug bezahlt ein Lehrer für 30 Schüler 135 Euro Eintritt ins Museum. Wie viel zahlt seine Kollegin mit ihrer Klasse von nur 28 Schülern?

Lösung: Proportionaler Dreisatz: (135 : 30) · 28 = 126 Euro

6. Aufgabe: Waschmaschine kaufen

Ein Elektrohändler bietet 15 Prozent Eröffnungsrabatt. Sie wollen eine Waschmaschine für 500 Euro kaufen. Was kostet sie abzüglich Rabatt?

Lösung: Prozent: (500: 100) · 15 = 75 Euro Rabatt. Die Waschmaschine kostet noch 425 Euro.

Was andere dazu gelesen haben

• Flächeninhalt Dreieck: Berechnung + Beispiele
• Primzahlen erkennen: Definition, Liste + Primfaktorzerlegung
• Zahl Pi (𝛑): Einfach erklärt + wie die Kreiszahl berechnen?
• Binomische Formeln auflösen: Erklärung, Übungen + Beispiele