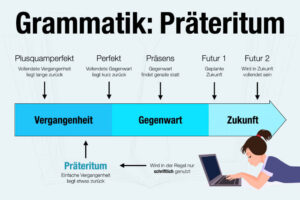
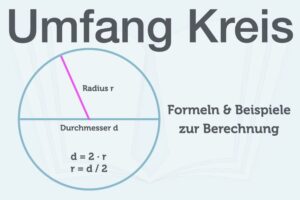
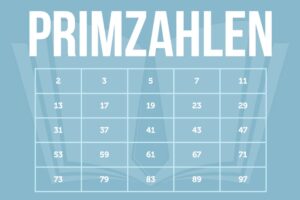
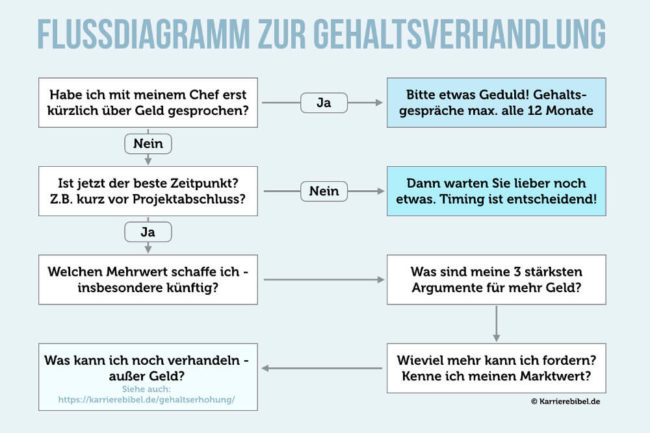
Wie lauten alle drei binomischen Formeln?
Die drei binomischen Formeln gehören in Mathe zur Algebra und erleichtern das Rechnen. Mit den Formeln können Sie Terme in Klammern, wie zum Beispiel (4 + 2)² einfach auflösen und ausmultiplizieren. Gleiches gilt für Rechnungen mit unbekannten Variablen wie (a + 4)².
Alle drei binomischen Formeln lauten:
- 1. binomische Formel: (a + b)² = a² + 2ab + b²
- 2. binomische Formel: (a – b)² = a² – 2ab + b²
- 3. binomische Formel: (a + b) • (a – b) = a² – b²
Erklärung: Binomische Formeln funktionieren in beide Richtungen – auch rückwärts, um mathematische Ausdrücke mit Klammern zu schreiben.
Achtung: In der Mathematik wird oft die vereinfachte Schreibweise genutzt: „ab“ steht für „a • b“. Beispiel: Statt „a • b + b • a“ können Sie auch „ab + ab“, kürzer: „2ab“ schreiben.
Binomische Formeln Übungen mit Lösung
Sie wollen die binomischen Formeln gleich üben? Dann finden Sie hier einige Übungen mit Lösung: Lösen Sie die Klammern mithilfe der binomischen Formeln auf. Für die Lösung: einfach aufklappen!
Übungen und Aufgaben (mit Lösung)
Lösung:
= (x + 7) · (x + 7)
= x² + 2 · x · 7 + 7²
= x² + 14x + 49 ✓
Lösung:
= (5b + 3r) · (5b + 3r)
= 5b² + 2 · 5b · 3r + 3r²
= 25b + 30br + 9r ✓
Lösung:
= (3x – 4y) · (3x – 4y)
= 3x² – 2 · 3x · 4y + 4y²
= 9x² – 24xy + 16y² ✓
Lösung:
= (a – 5) · (a – 5)
= a² – 2 · a · 5 + 5²
= a² – 10a + 25 ✓
Lösung:
= a² – 2a + 2a – 2²
= a² – 4 ✓
Lösung:
= x² – 9x + 9x – 9²
= x² – 81 ✓
Binomische Formeln: Übersicht + Übungen
Eine Übersicht der binomischen Formeln samt Übungen und Lösung können Sie sich hier kostenlos als PDF herunterladen:
Erste binomische Formel
Die erste binomische Formel wird auch „Plus-Formel“ genannt. Sie erkennen diese am Pluszeichen in der Klammer, das a und b miteinander verbindet. Sie lautet:
(a + b)² = a² + 2ab + b²
Die erste binomische Formel lässt sich wie folgt auflösen:
(a + b)²
= (a + b) • (a + b)
= a • (a + b) + b • (a + b)
= a² + a • b + b • a + b²
= a² + ab + ab + b²
= a² + 2ab + b²
Erste binomische Formel Beispiel
Binomische Formeln helfen bei Rechnungen mit einem Exponenten (zum Quadrat, hoch Zwei). Dabei werden die Zahlen in Klammern zuerst mit sich selbst multipliziert. Beispiele für Aufgaben:
(3 + 4)² = 3² + 2 • 3 • 4 + 4² = 9 + 24 + 16 = 49
(1 + 2)² = 1² + 2 • 1 • 2 + 2² = 1 + 4 + 4 = 9
Dieselbe Rechnung machen Sie, bei Aufgaben mit Variablen oder gemischt aus Zahlen und Buchstaben:
(2 + a)² = 2² + 2a • 2a + a² = 4 + 4a + a²
Herleitung der Plus-Formel
Letztlich helfen binomische Formeln dabei, das Auflösen von Klammern zu vereinfachen. Sie können die Rechnung aber genauso Schritt für Schritt herleiten und dabei die mathematischen Regeln anwenden:
(a + b)² = (a + b) • (a + b) = a (a + b) + b (a + b) = a² + a • b + b • a + b² = a² + ab + ab + b² = a² + 2ab + b²
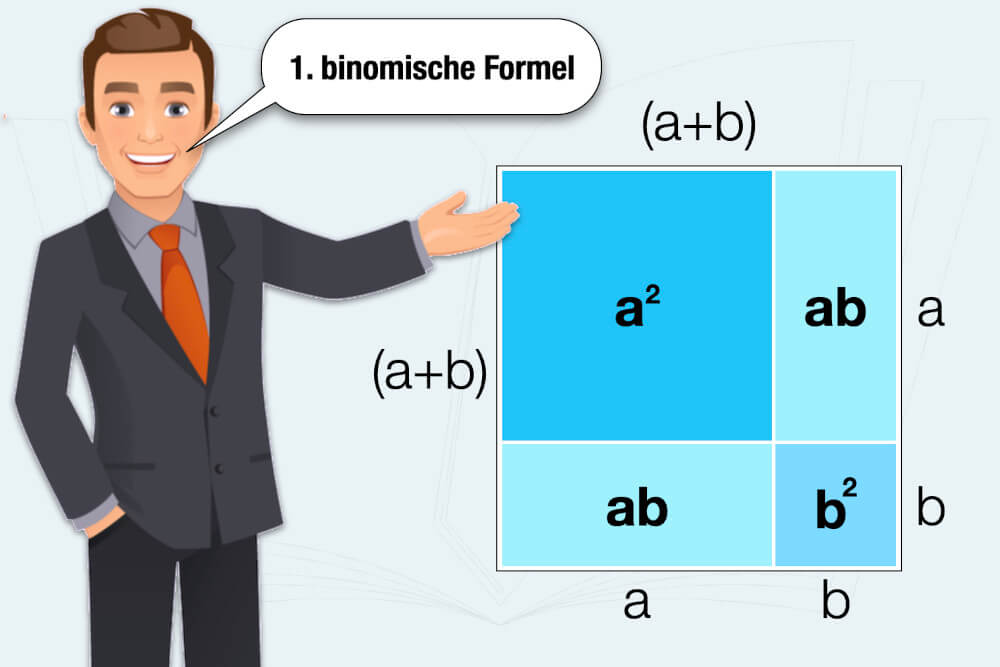
Zur geometrischen Veranschaulichung der 1. binomischen Formel hilft die folgende Grafik: Das schwarze Quadrat mit der Seitenlänge a + b lässt sich mit den beiden Quadraten a² und b² ausfüllen. Übrig bleiben jeweils zwei gleich große Rechtecke a • b (= ab).
Zweite binomische Formel
Die zweite binomische Formel wird auch „Minus-Formel“ genannt. Sie erkennen diese am Minuszeichen in der Klammer, das a und b miteinander verbindet. Sie lautet:
(a – b)² = a² – 2ab + b²
Die zweite binomische Formel lässt sich wie folgt auflösen:
(a – b)²
= (a – b) • (a – b)
= a • (a – b) – b • (a – b)
= a² – a • b – b • a – b²
= a² – ab – ab + b²
= a² – 2ab + b²
Zweite binomische Formel Beispiel
Auch mithilfe der zweiten binomischen Formel können Sie die Klammern wieder ganz einfach auflösen. Beispiele zur Formel:
(4 – 2)² = 4² – 2 • 4 • 2 + 2² = 16 – 16 + 4 = 4
(2 – 1)² = 2² – 2 • 2 • 1 + 1² = 1²
Dieselbe Rechnung funktioniert mit Variablen oder Zahlen:
(3 – a)² = 3² – 2 • 3 • a + a² = 9 – 6a + a²
Herleitung der Minus-Formel
Wenn Sie mögen, können Sie die zweite binomische Formel wieder einfach durch schrittweises Ausmultiplizieren herleiten und ausrechnen:
(a – b)² = (a – b) • (a – b) = a (a – b) – b (a – b) = a² – a • b – b • a + b² = a² – 2ab + b²
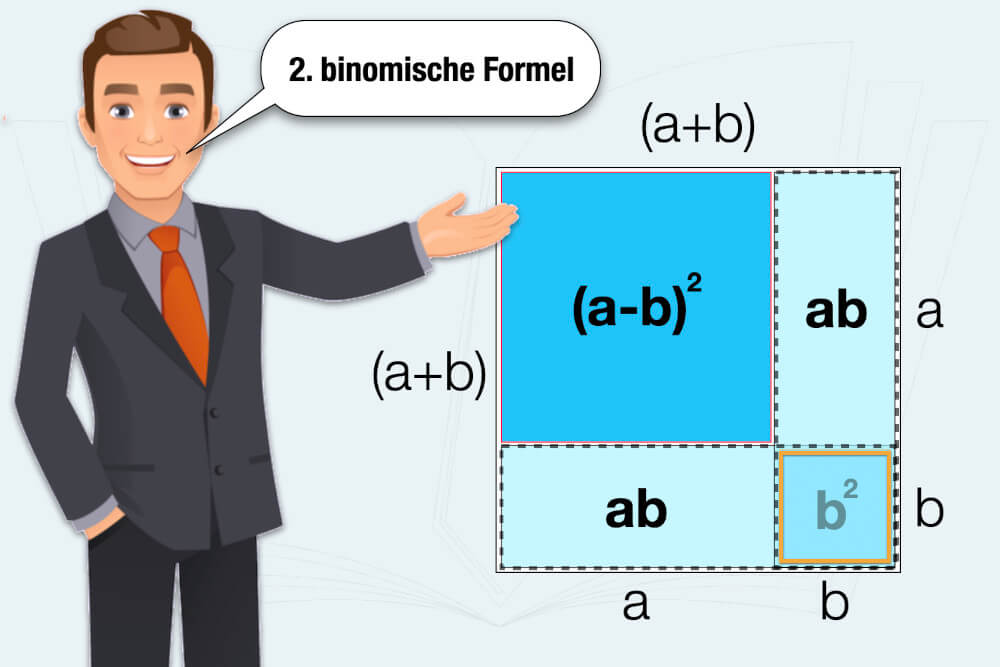
Auch diese Formel lässt sich durch die folgende Grafik veranschaulichen: Ausgangspunkt ist das große schwarz umrandete Quadrat. Von dort wollen Sie zum kleineren, rot umrandeten Quadrat (a – b)² gelangen. Dafür müssen Sie die beiden Rechtecke a • b abziehen. Weil Sie dann das kleine orangefarbene Quadrat b² doppelt abgezogen haben, korrigieren Sie die Rechnung, indem Sie b² einmal wieder hinzufügen.
Dritte binomische Formel
Die dritte binomische Formel ist eine Mischung aus den beiden vorherigen Formeln und wird auch „Plus-Minus-Formel“ genannt. Bei dieser Formel müssen Sie eine Klammer mit Pluszeichen mit einer Klammer mit Minuszeichen verrechnen. Sie lautet:
(a + b) • (a – b) = a² – b²
Die dritte binomische Formel lässt sich wie folgt auflösen:
(a + b) • (a – b)
= a • (a – b) + b • (a – b)
= a • a – a • b + b • a + b (- b)
= a² – a • b + b • a – b²
= a² – ab + ab – b²
= a² – b²
Dritte binomische Formel Beispiel
Die dritte der binomischen Formeln ist die einfachste. Die folgenden Beispiele zeigen, wie Sie die Klammern auflösen können:
(3 + 1) • (3 – 1) = 3² – 1² = 9 – 1 = 8
(4 + 3) • (4 – 3) = 4² – 3² = 16 – 9 = 7
Genauso verfahren Sie wieder beim Auflösen mit Variablen bzw. Buchstaben:
(5 + b) • (5 – b) = 5² – b² = 25 – b²
Herleitung der Plus-Minus-Formel
Alle binomischen Formeln funktionieren mit Buchstaben oder Zahlen. Entsprechend lässt sich auch die dritte binomische Formel nach den mathematischen Grundregeln auflösen:
(a + b) • (a – b) = a • (a – b) + b • (a – b) = a² – a • b + b • a – b² = a² – b²
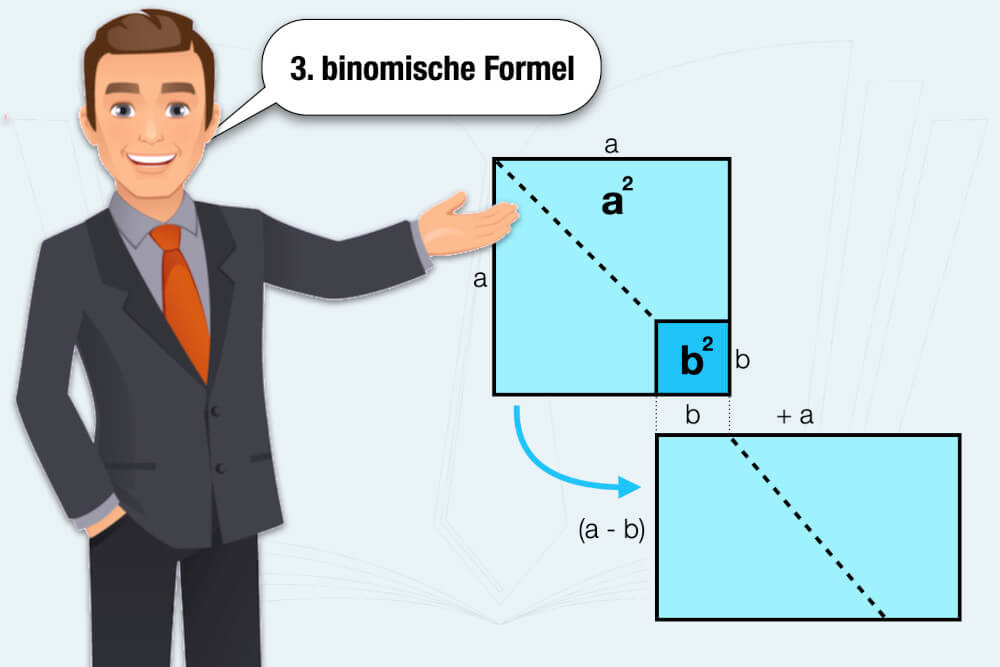
Zum besseren Verständnis veranschaulichen wir auch die 3. binomische Formel mit einer einfachen Grafik: In diesem Fall wollen Sie vom großen Quadrat (a²) das kleinere Quadrat (b²) abziehen.
Dazu teilen Sie die Fläche von a² diagonal entlang der gestrichelten Linie und fügen die verbleibenden Flächen verdreht wieder zusammen. Die neue Fläche entspricht senkrecht der Höhe (a – b) und waagerecht der Länge (a + b).
Binomische Formeln hoch 3
Alle drei binomische Formeln erleichtern das Rechnen mit Variablen und Buchstaben und ersparen auch noch zahlreiche Zwischenschritte.
Neben den Formeln mit der Hochzahl 2 gibt es Rechnungen mit höheren Exponenten wie 3, 4 oder 5. Grundlage bleiben aber die bekannten Formeln. Die „Erste binomische Formel hoch 3“ lautet daher:
(a + b)³ = a³ + 3a²b + 3ab² + b³
Auflösung mit Exponent 3
Die Herleitung der Formel mit der Hochzahl 3 funktioniert ähnlich wie die Auflösung der ersten binomischen Formel zum Quadrat:
(a + b)³
= (a + b) • (a + b) • (a + b)
= (a + b) • (a² + ab + ba + b² )
= (a + b) • (a² + 2ab + b²)
= a • a² + a • 2ab + a • b² + b • a² + b • 2ab + b • b²
= a³ + 3ab² + 3a²b + b³
Binomische Formeln Merksatz
Je größer die Exponenten (= Potenzen), desto unübersichtlicher wird es, die Klammern aufzulösen. Einen eindeutigen Merksatz gibt es zwar nicht, wohl aber Gesetzmäßigkeiten. Vergleichen Sie die Formel hoch 3 mit der Formel hoch 4:
(a + b)³ = a³ + 3a²b + 3ab² + b³
(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴
Die erste und letzte Potenz entspricht immer dem Grad des Binoms. Zweitens nehmen die Potenzen der Variable „a“ von links nach rechts ab: a⁴, a³, a², a. Hingegen nehmen die Potenzen von „b“ von links nach rechts zu: b, b², b³, b⁴.
Was andere dazu gelesen haben
- Zahl Pi (𝛑): Einfach erklärt + wie die Kreiszahl berechnen?
- Römische Zahlen übersetzen: Regeln, Liste, Tabelle