Definition: Was ist die Zahl Pi?

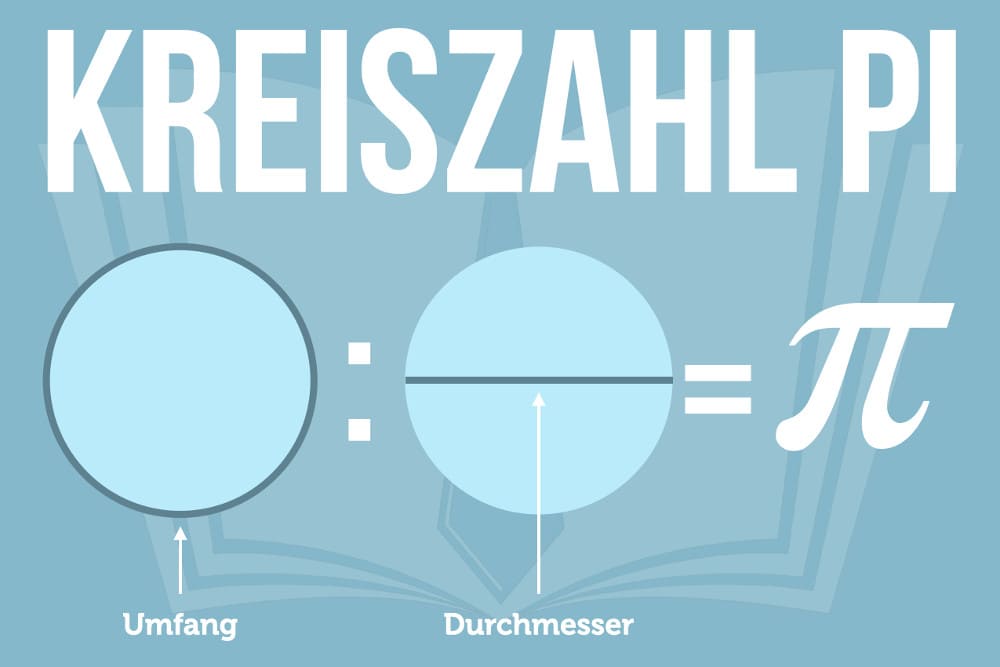
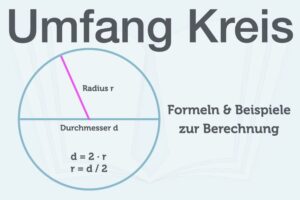
Die Zahl Pi (𝜋) beschreibt das Verhältnis vom Umfang eines Kreises (U) zu seinem Durchmesser (d). Als Formel ausgedrückt: 𝜋 = U/d. Der Kreisumfang ist immer 3,1415926535 und so weiter – egal, wie groß ein Kreis ist. Denn die Kreiszahl Pi ist eine mathematische Konstante.

Bedeutet: Pi ist eine unveränderliche Zahl und unendlich. Sie gehört zu den reellen, irrationalen Zahlen und lässt sich nie in ganzen Zahlen als Bruch darstellen, sondern nur als Dezimalzahl, die unendlich viele Nachkommastellen besitzt. Sie ist zudem nicht periodisch, bedeutet: Die Zahlenfolge nach dem Komma wiederholt sich nie.

Pi einfach erklärt

Zeichnen Sie mit einem Zirkel einen Kreis mit einem Durchmesser von einem Zentimeter. Um sich das Verhältnis von Umfang zum Durchmesser besser vorzustellen, rollen Sie den Kreisumfang einmal vollständig ab. Der zurückgelegte Weg (im unteren Beispiel die rote Linie) entspricht immer dem konstanten Wert 3,14… also der Kreiszahl Pi (𝜋):

Häufige Synonyme für die Zahl Pi sind: Kreiszahl, Ludolphsche Zahl oder Archimedes-Konstante. Die beiden letzten Bezeichnungen verweisen auf berühmte Mathematiker, die sich um die Erforschung und Berechnung der Zahl 𝜋 verdient gemacht haben.

Pi Symbol

Pi ist der 16. Buchstabe im griechischen Alphabet und wird mit dem Kleinbuchstaben 𝜋 dargestellt, der zugleich das Symbol für die Kreiszahl Pi ist. Der Grund: 𝜋 ist der Anfangsbuchstabe der griechischen Wörter περίμετρος (perímetros, Deutsch: „Umfang“) und περιφέρεια (peripheria, Deutsch: „Randbereich“). Den Buchstaben 𝜋 als Symbol für die Kreiszahl nutzte erstmals der englische Mathematiker William Oughtred im 17. Jahrhundert.

Verwechseln Sie die Zahl Pi nicht mit der Zahl Phi (Symbol: Φ)! Die Zahl Phi bezeichnet in der Mathematik den „goldenen Schnitt“ und bestimmt das Verhältnis der Teilung einer Strecke in zwei Teile. Dies stellt man mit der Formel a / b = ( a + b ) / a dar. Heraus kommt eine andere irrationale Zahl – ungefähr 1,6180339887.

Pi Zahl Nachkommastellen: 100 Stellen ausgeschrieben

Die Zahl Pi übt auf Mathematiker eine große Faszination aus: Zahlreiche Mathematiker haben im Laufe der Jahrtausende versucht, sich der Zahl anzunähern. Die ersten 100 Stellen nach dem Komma lauten ausgeschrieben:

𝜋 = 3.14159265358979323846264338327950288419716939937510
58209749445923078164062862089986280348253421170679821…

Zur Berechnung des Kreisumfangs reichen meist die ersten drei Nachkommastellen – also: 3,141 oder aufgerundet: 3,142. Dank moderner Computerberechnungen sind heute ganze 100 Billionen Nachkommastellen bekannt, sämtliche kennt aber niemand – außer Chuck Norris vielleicht.

Wofür braucht man Pi?

Kein Kreis, keine Kugel und keine Rundung ließe sich ohne Pi berechnen. In der Geometrie ist die Zahl Pi Bestandteil vieler mathematischer Formeln. Beispielsweise können Sie damit Folgendes berechnen:

Fläche eines Kreises
A = 𝜋∙r²
Umfang eines Kreises
U = 2∙𝜋∙r
Volumen einer Kugel
V = (4/3)⋅𝜋⋅𝑟³
Oberfläche eines Zylinders
O = (2⋅𝜋⋅𝑟²)+(2⋅𝜋⋅𝑟⋅ℎ)

Wichtig ist die Kreiszahl 𝜋 zudem in vielen anderen mathematischen Teilgebieten, etwa der Physik oder den Ingenieurwissenschaften.

Beispiel: Durchmesser berechnen mit Pi

Bis heute rechnen Schüler in der Schule bei Mathematikaufgaben mit der Kreiszahl Pi. Eine typische Textaufgabe lautet zum Beispiel:

Ein Förster will den Durchmesser (d) eines Baumstamms bestimmen. Mit einem Maßband misst er den Umfang (U) von 103 Zentimetern. Welchen Durchmesser hat der Stamm?

Die Formel zur Berechnung lautet: d = U/𝜋.
Lösung: Durchmesser = 103/𝜋, macht 32,79

Kreiszahl Pi lernen

Die Faszination für 𝜋 ist so groß, dass sich ein regelrechter Sport darum entwickelt hat. Es geht nicht nur darum, möglichst viele Nachkommastellen zu entdecken, sondern diese auch auswendig zu lernen. Viele greifen dafür zu bestimmten Mnemotechniken aus dem Gedächtnistraining.

Mit 70.000 aufgesagten Nachkommastellen gilt der Inder Rajveer Meena als offizieller Weltrekordhalter. Übertroffen wird er durch den inoffiziellen Weltrekord des Japaners Akira Haraguchi, der 100.000 Stellen fehlerfrei aufsagen konnte.

Eselsbrücke für Pi

Wer die ersten sieben Nachkommastellen von Pi lernen möchte, dem sei diese Eselsbrücke und der Satz empfohlen: „May I have a large container of coffee…“

Übrigens: Der 14. März gilt als internationaler „Pi-Tag“, weil das dem amerikanischen Datumsformat (3/14) entspricht.

Annäherung und Herleitung von Pi

Um möglichst exakte Bauwerke wie Getreidespeicher oder Wasserbecken erstellen zu können, griffen Menschen bereits in der Antike auf Berechnungen zurück, die der Kreiszahl ähneln. Der griechische Mathematiker Archimedes von Syrakus war im 3. Jahrhundert v. Chr. der Erste, der den heutigen Zahlenwert von Pi bestimmte. Für seine Annäherung an Pi nutzte er sog. Vielecke und einen Kreis mit dem Radius 1.

Zunächst zeichnete Archimedes ein Sechseck in den Kreis und berechnete den Umfang des Sechsecks, dessen Eckpunkte exakt auf der Kreislinie lagen. Diese Berechnungen waren aber nie exakt, weil sie nicht alle Punkte der Kreislinie erfassten. Deshalb wiederholte Archimedes seine Berechnungen mit einem 12-, 24-, 48- und 96-Eck. Danach ermittelte er die Werte für den Umfang von Vielecken, die außerhalb des Kreises lagen. Archimedes konnte so eine Ober- und Untergrenze für Pi berechnen und den Wert auf zwei Nachkommastellen genau bestimmen.

Ludolph van Ceulen

Das Mittelalter führt in Europa dazu, dass viel mathematisches Wissen aus der Antike in Vergessenheit geriet. Erst der deutsch-niederländische Mathematiker Ludolph van Ceulen machte im 16. Jahrhundert wieder Fortschritte bei der Erforschung der Zahl Pi. Er kam mit seinen Berechnungen schon auf 35 Nachkommastellen, weshalb die Kreiszahl bis ins 19. Jahrhundert als Ludolphsche Zahl bekannt war.

Was andere dazu gelesen haben