Flächeninhalt Dreieck

Als Dreieck bezeichnet man in der Geometrie eine Figur mit drei Ecken. Verbunden sind die Ecken über die Seiten des Dreiecks. Zum Flächeninhalt eines Dreiecks zählen alle Punkte innerhalb des Dreiecks sowie auf den Verbindungslinien.

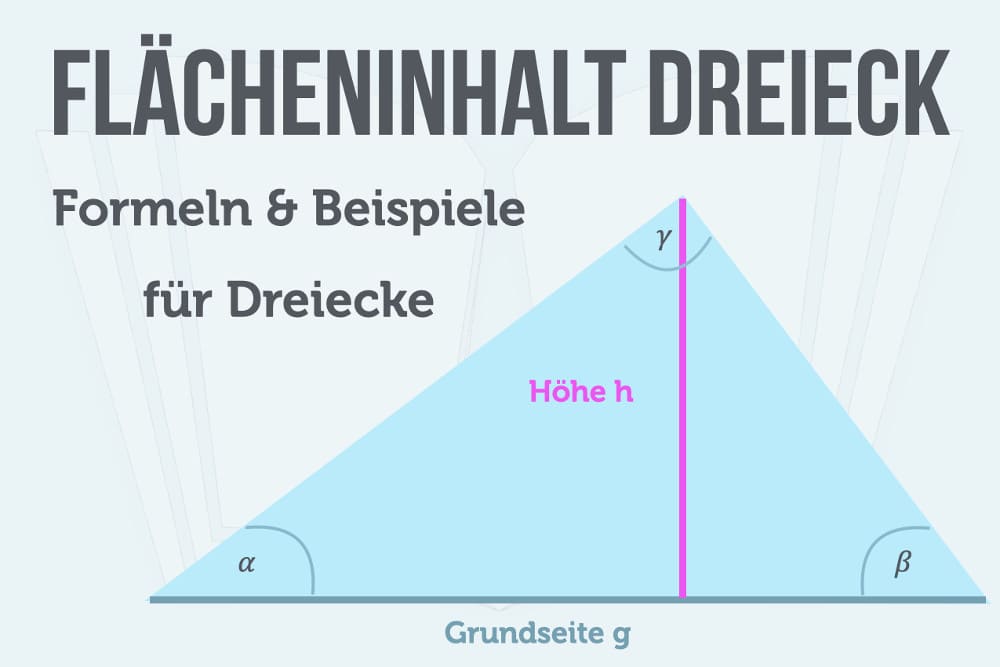
Am einfachsten können Sie den Flächeninhalt berechnen, wenn Sie Angaben zur Höhe und zur Grundseite eines Dreiecks haben. Folgende Grafik verdeutlicht das anhand eines Beispiels. Darin beträgt die Höhe (h) 4 Zentimeter und die Grundseite (g) 9 Zentimeter.

Flächeninhalt Dreieck mit Formel berechnen

Der Flächeninhalt wird in der Mathematik meist mit dem Buchstaben A (teilweise auch F) angegeben. Der Kleinbuchstabe g steht für die Grundseite (auch Grundlinie), das ist bei grafischen Darstellungen die untere Seite eines Dreiecks. Der Kleinbuchstabe h bezeichnet die Höhe.

Mit diesen Angaben können Sie leicht den Flächeninhalt eines Dreiecks berechnen. Dazu multiplizieren Sie die Länge der Grundseite g mit der Höhe h und teilen das Ganze durch 2. Als Formel lässt sich das so darstellen:

A = ½ ∙ g ∙ h

Auf unser obiges Beispiel angewandt heißt das:

A = ½ ∙ 9 cm ∙ 4 cm

Ausgerechnet erhalten Sie:

A = 18 cm².

Wichtig: Multiplizieren Sie Zentimeter mit Zentimeter, erhalten Sie Quadratzentimeter als Ergebnis. Daher müssen Sie hoch 2, also cm² schreiben.

Alternative Schreibweise
Die obige Formel gilt für allgemeine Dreiecke, bei denen Sie eine Grundfläche g haben. Häufig wird die dem Eckpunkt (markiert mit dem Großbuchstaben A, B oder C) gegenüberliegenden Seite mit einem Kleinbuchstaben bezeichnet. So finden Sie die Seiten a, b und c anstelle von g.

Zudem kann jeder Seite eine Höhe zugeordnet werden. Entsprechend existieren andere Schreibweisen der Formel, die aber zum gleichen Ergebnis führen:

A = ½ ∙ g ∙ h (= ½ ∙ a ∙ h_a = ½ ∙ b ∙ h_b = ½ ∙ c ∙ h_c)

Beispiel Flächeninhaltsberechnung Dreieck

Genauso wie beschrieben gehen Sie mit anderen Dreiecken um. Sie haben beispielsweise ein Dreieck mit den Seitenlängen g = 6 cm und h = 5 cm. Folgendermaßen können Sie den Flächeninhalt berechnen:

1. Schritt: Formel rekapitulieren
A = ½ ∙ g ∙ h

2. Schritt: Angaben einsetzen
A = ½ ∙ 6 cm ∙ 5 cm

3. Schritt: Flächeninhalt ausrechnen
A = 15 cm²

Flächeninhalt Dreieck mit Angaben umrechnen

Die bisherigen Beispiele ließen sich mühelos berechnen, da die Angaben jeweils in der gleichen Maßeinheit (Zentimeter) vorlagen. Obige Formel zur Berechnung des Flächeninhalts eines Dreiecks können Sie auch bei Aufgaben mit unterschiedlichen Maßeinheiten anwenden.

Voraussetzung dafür ist allerdings, dass Sie zuvor die Angaben entsprechend umrechnen. Sie haben beispielsweise ein Dreieck mit den Seitenlängen g = 70 mm und h = 0,5 cm. Dann schalten Sie vor die obigen drei Schritte noch einen Schritt vor:

1. Schritt: Angaben umrechnen
mm = Millimeter; g = 70 mm = g = 7 cm

2. Schritt: Formel rekapitulieren
A = ½ ∙ g ∙ h

3. Schritt: Angaben einsetzen
A = ½ ∙ 7 cm ∙ 5 cm

4. Schritt: Flächeninhalt ausrechnen
A = 17,5 cm²

Flächeninhalt Dreieck Rechner

Wem die Formeln zu kompliziert und das Rechnen zu umständlich ist, der kann den Flächeninhalt vom Dreieck mit einem Rechner berechnen. Voraussetzung dafür ist, dass Sie wenigstens drei Werte eingeben.

Auszufüllende Werte können beispielsweise Angaben zur Höhe, Seitenlänge oder Winkel sein. Einen solchen Rechner finden Sie HIER von der Seite mathepower.com.

Flächeninhalt Dreieck ohne Höhe (mit rechtem Winkel)

In einem rechtwinkeligen Dreieck ist ein Winkel exakt 90° groß. Während Sie für viele Dreiecke zunächst eine Höhe festlegen müssen, ist es bei einem rechtwinkeligen Dreieck recht simpel. Hier rechnen Sie einfach mit den beiden Seiten, die den 90°-Winkel einschließen: das sind die beiden Katheten a und b.

Formel für rechtwinkliges Dreieck

Für den Flächeninhalt eines rechtwinkligen Dreiecks benötigen Sie folgende Formel:
A = ½ ∙ a ∙ b

Diese Formel können Sie auch umstellen, wenn Sie beispielsweise eine Seitenhöhe oder eine Seitenlänge berechnen wollen:

a = (A · 2) / b

Oder:

b = (A · 2) / a

Flächeninhalt Dreieck gleichschenkelig

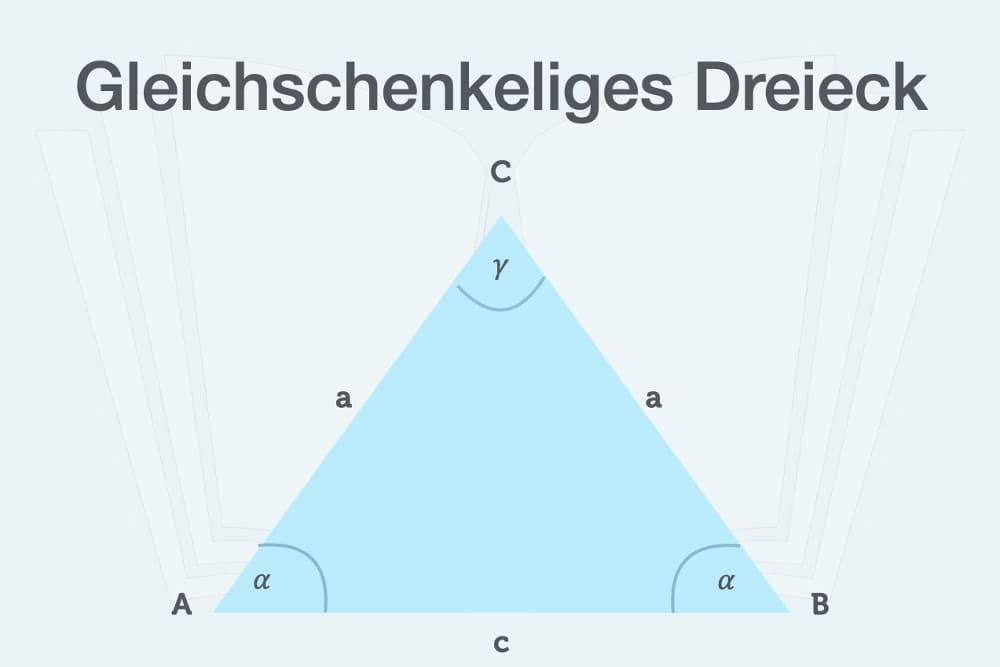
Merkmal eines gleichschenkeligen Dreieck sind zwei gleich lange Seiten, genannt Schenkel. Die dritte Seite ist die Basis. Üblicherweise benennt man die Ecken mit den Großbuchstaben A, B und C. Die jeweils gegenüberliegende Seite erhält den passenden Kleinbuchstaben a, b oder c. Da beim gleichschenkeligen Dreieck zwei Seitenlängen identisch sind, erhalten beide Schenkel die Bezeichnung a. Die Basis wird mit c gekennzeichnet, da Sie der Spitze C gegenüberliegt.

Formel für gleichschenkeliges Dreieck

Für den Flächeninhalt eines gleichschenkeligen Dreiecks benötigen Sie folgende Formel:

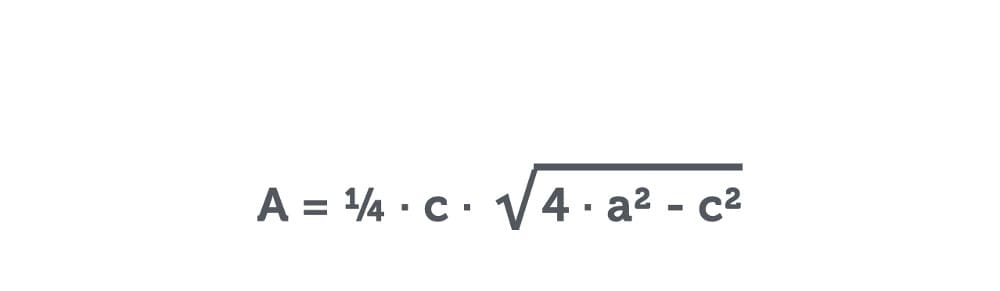
Flächeninhalt Dreieck gleichseitig

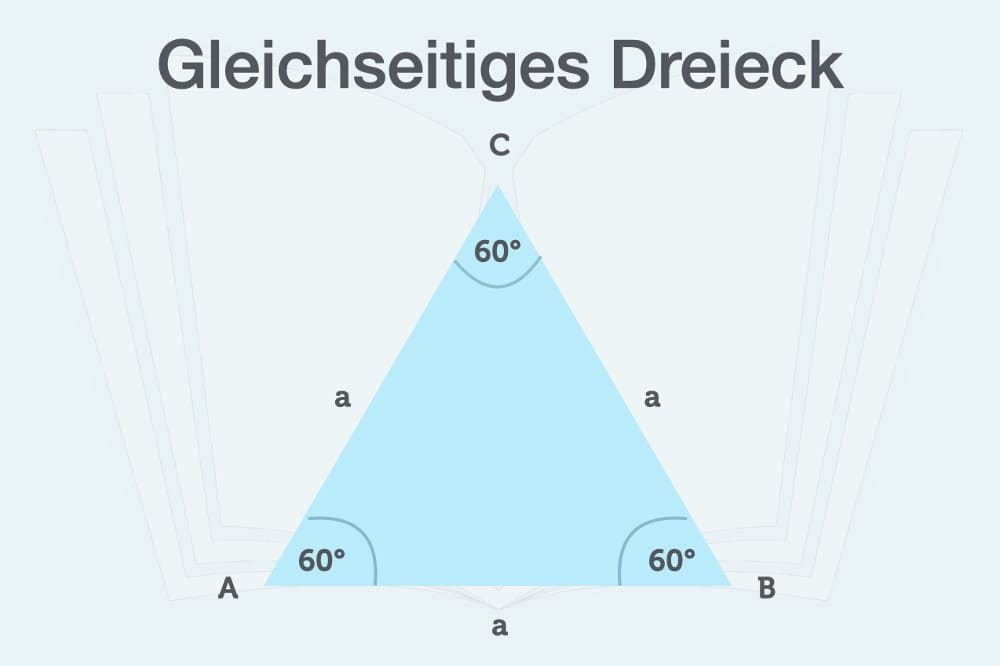
Das gleichseitige Dreieck zeichnet sich durch drei gleich lange Seiten aus. Die Summe aller Winkel in einem Dreieck ergibt immer 180°. Das Besondere am gleichseitigen Dreieck: Hier sind alle Winkel gleich groß. Jeder Winkel beträgt 60 Grad.

Formel für gleichseitiges Dreieck

Da alle Seiten gleich lang sind, gibt es für die Formel des Flächeninhalts nur den Buchstaben a. Die Formel zur Flächeninhaltsberechnung lautet:

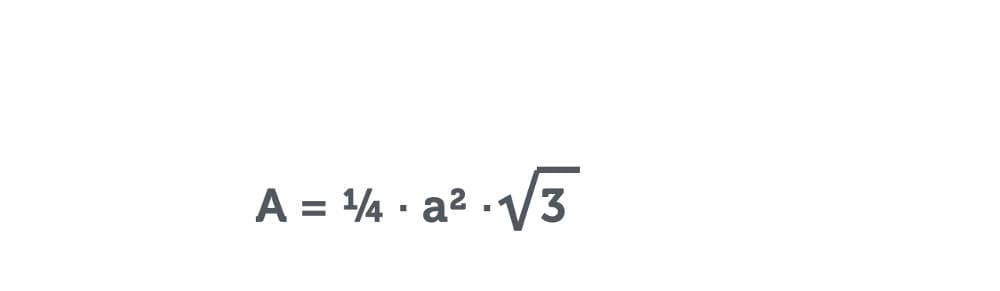
Flächeninhalt Dreieck stumpfwinklig

Der Vollständigkeit halber sei noch das stumpfwinklige Dreieck erwähnt. Das Besondere daran ist, dass es einen stumpfen Winkel hat. Das bedeutet, dass ein Winkel im Dreieck größer als 90°, aber kleiner als 180° sein muss. Die beiden anderen Winkel sind spitz und ergeben zusammen immer weniger als 90°. Jeder Winkel kann ein stumpfer Winkel sein – 𝛼, 𝛽 oder 𝛾. In der nachfolgenden Grafik ist das 𝛼.

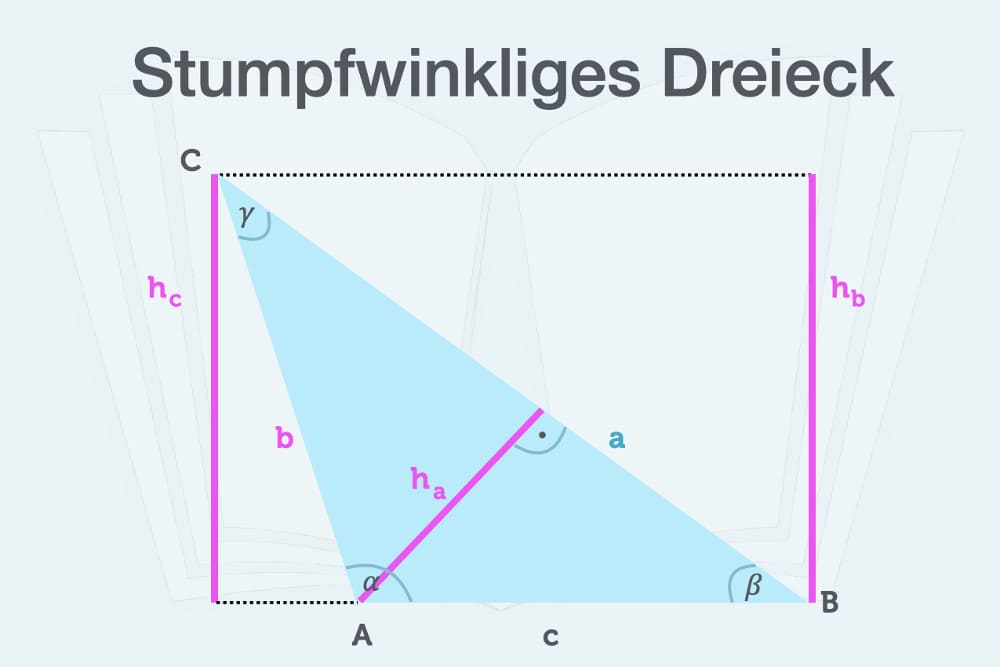
Zu den weiteren Eigenschaften zählt, dass die Seiten immer unterschiedlich lang sind. Wären alle drei Seiten gleich lang, läge ein spitzwinkliges Dreieck vor. Das stumpfwinklige Dreieck kann aber gleichschenkelig sein, also zwei gleich lange Seiten haben.

Formel für stumpfwinkliges Dreieck

Den Flächeninhalt eines stumpfwinkligen Dreiecks können Sie mit folgender Formel berechnen:

A = ½ ∙ a ∙ h

Oder:

A = ½ ∙ a ∙ b ∙ sin 𝛾

Dabei müssen Sie beachten, welche Höhe Sie berechnen wollen: Das ist immer die Senkrechte auf der Grundlinie, die zum gegenüberliegenden Eckpunkt (A, B oder C) verläuft. In der obigen Abbildung also h_a, h_b oder h_c.

Herleitung der Formel

Um den Flächeninhalt eines Dreiecks berechnen zu können, braucht man zunächst zwei Längen, die senkrecht zueinander stehen – so wie bei der Berechnung von Rechtecken. Anders als bei einem Dreieck ist das beim Rechteck automatisch gegeben. Bei einem Dreieck kann man nicht einfach zwei Seiten miteinander multiplizieren. Aber es gibt eine Krücke: Wir denken uns zunächst ein Rechteck um das Dreieck, bei dem die Ecken exakt auf den Seitenlinien liegen.

Die Grundseite dieses Rechtecks hat die gleiche Länge wie das Dreieck. Die andere Seite ist mit der Höhe h identisch. Damit haben wir eine Seite, die senkrecht zur Grundseite g steht.

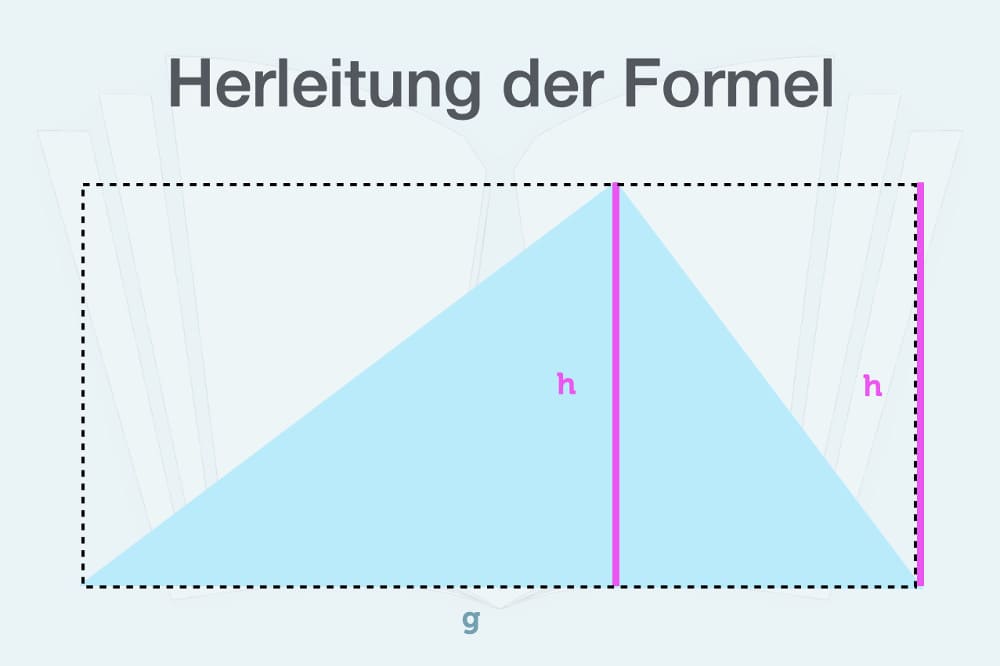
Die Höhe teilt ein beliebiges Dreieck in zwei Dreiecke mit rechtem Winkel. Die dem rechten Winkel gegenüberliegende Seite nennt sich Hypotenuse. Spiegelt man nun die beiden Dreiecke jeweils an ihrer Hypotenuse, erhält man ein Rechteck. Grafisch sieht das folgendermaßen aus:

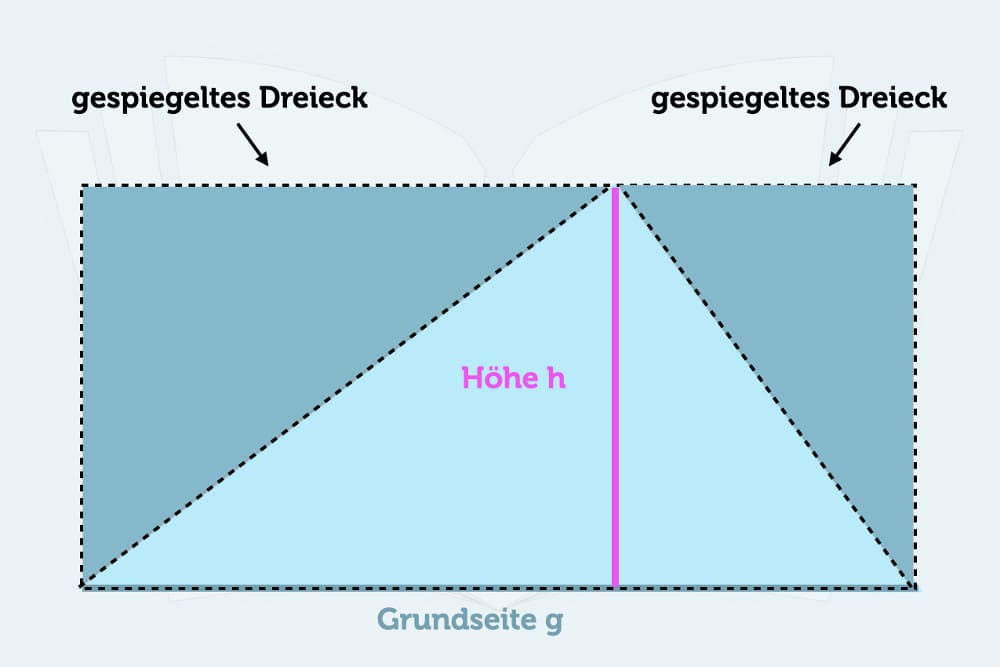
Die dunkleren Dreiecke entsprechen in den Maßen absolut den beiden helleren Teildreiecken. Den Flächeninhalt eines Rechtecks erhält man, indem man die Grundseite mit der Seitenlänge multipliziert („Länge mal Breite“). Als Formel ausgedrückt schreibt man:
A = g ∙ h

Halbieren des Rechtecks

Das ursprüngliche Dreieck entspricht exakt der Hälfte dieses Rechtecks, da wir zuvor die Teilhälften des Dreiecks verdoppelt haben. Die Formel zur Berechnung des Quadrats eignet sich nicht, weil wir den doppelten Flächeninhalt bekämen.

Also müssen wir die Formel zur Berechnung eines Rechtecks durch 2 teilen – daher auch der Bruch in der Rechnung. Somit ergibt sich zur Berechnung des Flächeninhalts des ursprünglichen Dreiecks folgende Formel:

A = ½ ∙ Grundseite ∙ Höhe, also A = ½ ∙ g ∙ h

Sie können diese Formel auch umstellen, wenn Sie beispielsweise einen anderen Wert wie die Höhe oder Seitenlänge ausrechnen wollen:

h = (A · 2) / g

Oder:

g = (A · 2) / h

Flächeninhalt Dreieck mit Sinus berechnen

Um ein Dreieck berechnen zu können, brauchen Sie immer drei Größen. Mit diesen drei Werten können Sie einen vierten errechnen. Was aber, wenn Sie nur zwei Seiten eines Dreiecks kennen? Hier kann der Sinussatz helfen. Dafür benötigen Sie als Angaben beispielsweise zwei Seiten und einen Winkel. Dann können Sie den gegenüberliegenden Winkel berechnen. Oder Sie kennen zwei Winkel und eine Seite, dann können Sie die andere Seite berechnen.

Sinus Formeln

Die dazugehörige Formel lautet:

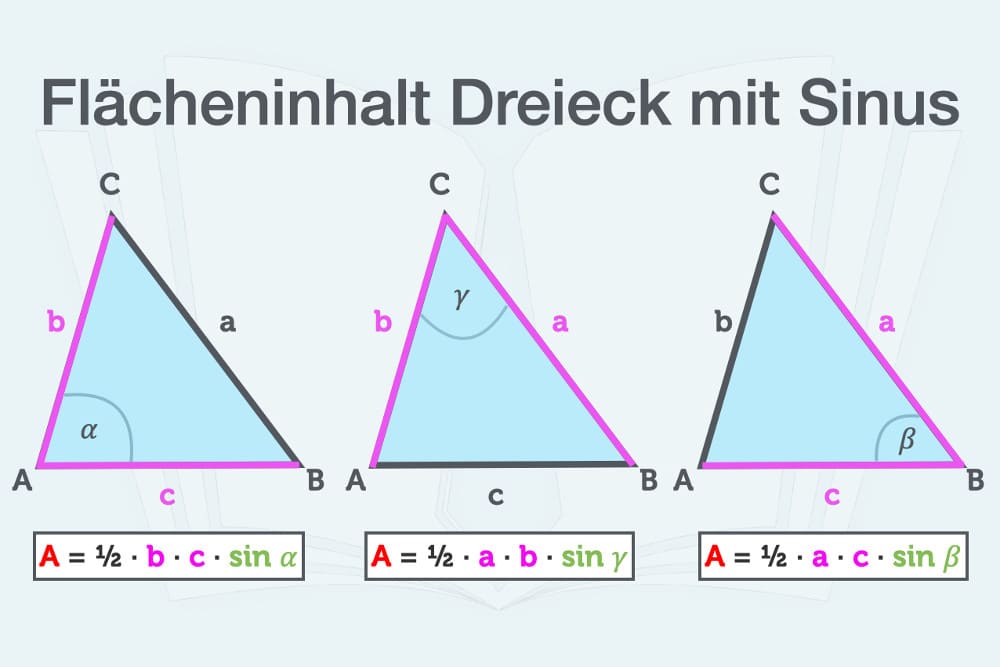
A = ½ · a · b · sin 𝛾

Da Sie anstelle von 𝛾 auch mit einem anderen Winkel rechnen können, kann alternativ eine der beiden folgenden Formeln zum Einsatz kommen:

A = ½ · a · c · sin 𝛽

Oder:

A = ½ · b · c · sin 𝛼

Aufgaben zum Flächeninhalt vom Dreieck

Nachfolgend haben wir einige Aufgaben für Sie. Die Fragen und Übungen sollten Sie lösen können, wenn Sie den Flächeninhalt eines Dreiecks berechnen wollen. Die Auflösung dazu können Sie kostenlos mit einem Klick auf den Button als PDF herunterladen.

Benennen Sie die Seiten, Winkel und Eckpunkte eines Dreiecks.
Berechnen Sie den Flächeninhalt eines Dreiecks mit a = 5 Zentimetern und b = 6 Zentimetern.
Wie groß ist der Flächeninhalt eines rechtwinkligen Dreiecks, wenn die Katheten 3 und 2 Zentimeter lang sind?
Sie haben ein Dreieck mit den Seiten a und b. Seite a ist 35 Millimeter lang, b ist 4 Zentimeter lang. Errechnen Sie den Flächeninhalt.
Wie groß sind die beiden Winkel in einem gleichschenkligen Dreieck, wenn es einen rechten Winkel hat?

Lösung Flächeninhalt Dreieck (PDF)

Lesen Sie weiter, wenn Sie den Umfang eines Kreises berechnen wollen.

Was andere Leser dazu gelesen haben

[Bildnachweis: Karrierebibel.de]