Umfang Kreis: Durchmesser, Flächeninhalt + Kreisumfang

Definition + Formel: Kreis und Bestandteile

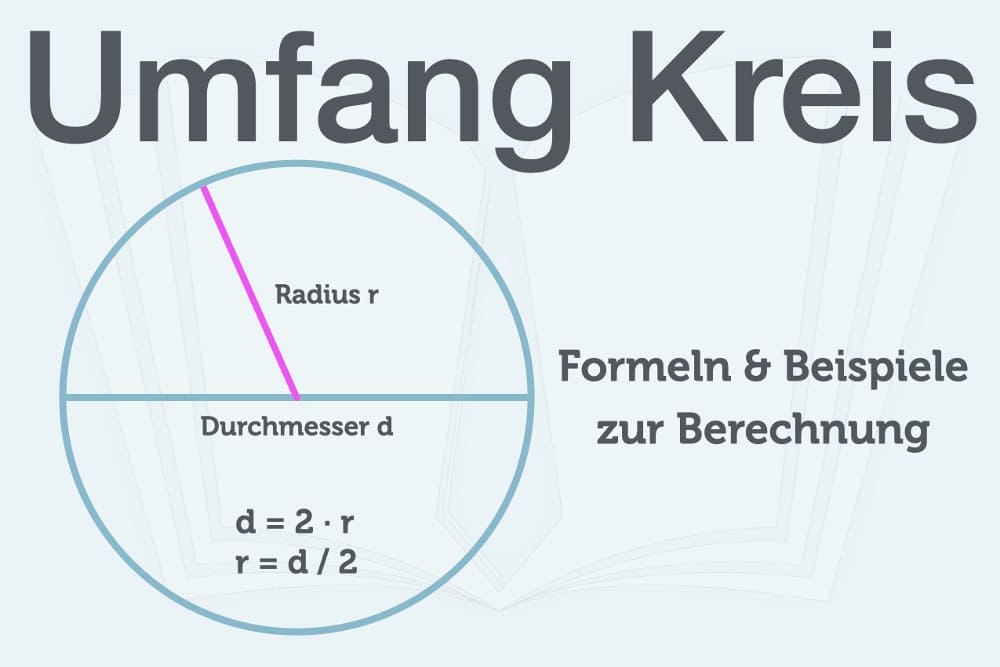
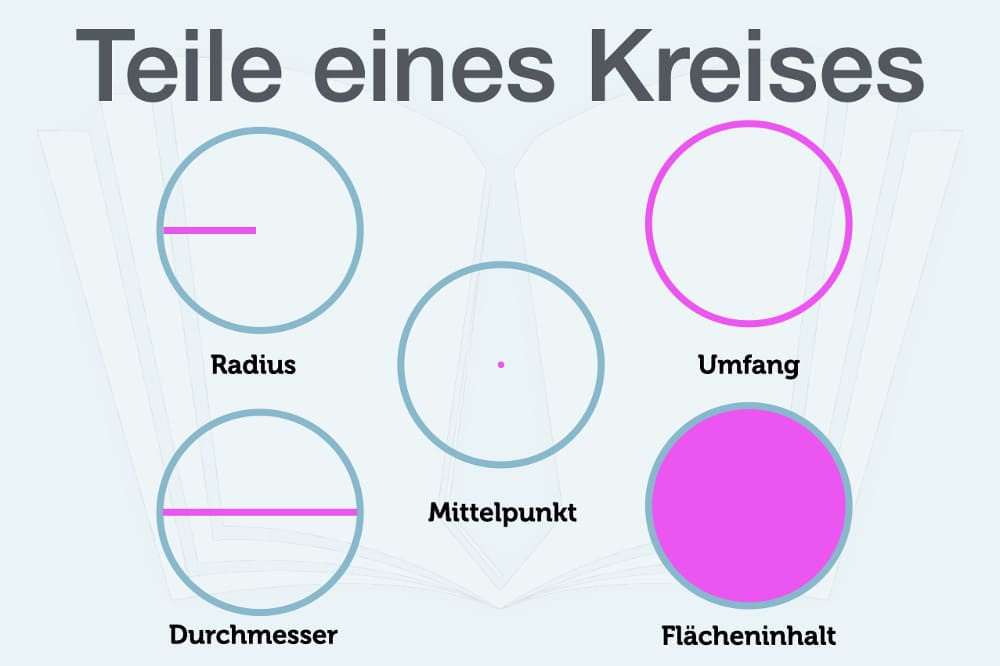
Ein Kreis ist eine geometrische Figur. Bei seiner runden Fläche sind die Punkte auf dem Kreisrand allesamt gleich weit vom Zentrum entfernt. Das Zentrum bezeichnet man als Mittelpunkt M. Die Bestandteile eines Kreises werden folgendermaßen definiert:

Umfang

Der Umfang u ist die Länge der Kreislinie.

Radius

Der Abstand eines Punktes auf der Kreislinie zum Mittelpunkt ist der Radius r. Er heißt auch Halbmesser.

Durchmesser

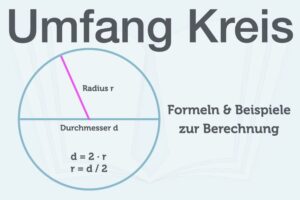
Die doppelte Länge heißt Durchmesser d. Der Kreisdurchmesser ist die längste Strecke zweier Punkte durch den Mittelpunkt. Als mathematische Formel lässt sich das folgendermaßen darstellen: d = 2r oder r = d/2

Flächeninhalt

Als Kreisfläche A bezeichnet man die Fläche, welche von der Kreislinie umschlossen wird.

Umfang Kreis berechnen: Durchmesser oder Radius

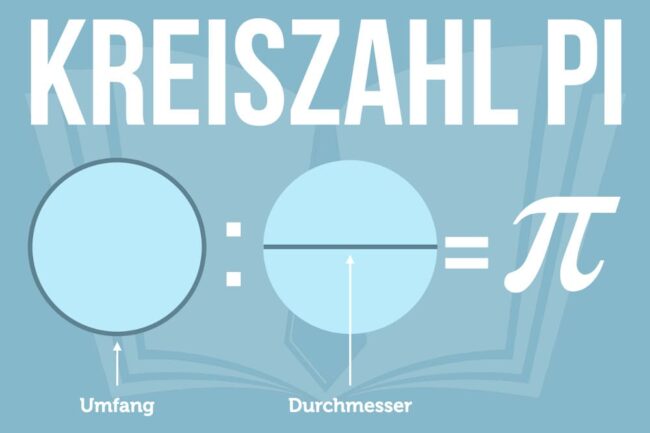
Will man den Umfang von einem Kreis berechnen, öffnet man ihn gedanklich und misst die begradigte Kreislinie. Zur Berechnung benötigen Sie einen Wert wie den Durchmesser oder Radius und die Zahl Pi (𝜋).

Die Kreiszahl Pi besitzt unendlich viele Nachkommastellen, wird aber meist auf zwei Nachkommastellen abgekürzt. Somit ergibt sich 𝜋 = 3,14. Der Kreisumfang ist immer 3,14 mal größer als sein Durchmesser.

Umfang Kreis berechnen mit Durchmesser

Kennen Sie beispielsweise den Durchmesser eines Kreises, müssen Sie den Wert lediglich in die folgende Formel einsetzen:

u = 𝜋 ∙ d

1. Beispiel

Für unser Beispiel beträgt der Durchmesser 4 Zentimeter. Dafür rechnen Sie:

u = 𝜋 ∙ 4 cm
= 3,14 ∙ 4 cm
= 12,56 cm.

Aufgerundet beträgt der Kreisumfang also 12,6 Zentimeter.

2. Beispiel: 21 cm Durchmesser, Umfang berechnen

u = 𝜋 ∙ 21 cm
= 3,14 ∙ 21 cm
= 65,94 cm.

Leicht abgerundet liegt der Kreisumfang bei 65,9 Zentimetern.

Umfang Kreis berechnen mit Radius

Ebenso einfach lässt sich der Umfang vom Kreis berechnen, wenn Sie den Radius als Wert haben. Die Formel zur Berechnung des Kreisumfangs lautet hier: u​ = 2 ∙ 𝜋 ∙ r

Beispiel

Für unser Beispiel ist ein Radius mit 7,5 Zentimetern gegeben. Sie rechnen folgendermaßen:

u​ = 2 ∙ 𝜋 ∙ 7,5 cm
= 2 ∙ 3,14 ∙ 7,5 cm
= 47,1 cm.

Der Kreisumfang liegt bei 47,1 Zentimetern.

Kreisfläche Formel + Berechnung

Die Kreisfläche A ist vollständig von der Kreislinie umschlossen. Um sie zu berechnen, multiplizieren Sie das Quadrat des Radius mit der Kreiszahl Pi. Die Formel lautet:

A = r² ∙ 𝜋

Beispiel

Im nachfolgenden Beispiel beträgt der Radius 5 Zentimeter. Sie rechnen folgendermaßen:

A = 5 cm² ∙ 𝜋
= 5 cm² ∙ 3,14
= 78,5 cm²

Als Ergebnis erhalten Sie also eine Kreisfläche von 78,5 Quadratzentimetern.

Umfang Kreis: Formel umstellen

Wollen Sie den Umfang eines Kreises berechnen und haben als Wert nur die Fläche, müssen Sie einen Zwischenschritt einlegen. Dann wollen Sie beispielsweise den Radius r herausfinden, um den Umfang zu berechnen.

Die Formel für den Flächeninhalt A = r² ∙ 𝜋 müssen Sie umstellen, indem Sie nach r auflösen. Anschließend verfahren Sie wie im obigen Beispiel. Zur Berechnung der Kreisfläche verwenden Sie folgende Formel:

r = √ (A / 𝜋)

Beispiel

Beispielsweise haben Sie eine Kreisfläche von 38,5 Quadratzentimetern. Dann tragen Sie den Wert in die Formel ein:

r = √ (38,5 cm / 𝜋)
= √ (38,5 cm / 3,14)
= √ (12,27)
= 3,50 cm.

Da Sie die Wurzel ziehen, wandeln Sie Quadratzentimeter in Zentimeter um. Der Radius beträgt somit (leicht abgerundet) 3,50 Zentimeter. Mit diesem Wert können Sie nun den Umfang berechnen:

u​ = 2 ∙ 𝜋 ∙ 3,5 cm
= 2 ∙ 3,14 ∙ 3,5 cm
= 21,98 cm

Der Kreisumfang beträgt (leicht aufgerundet) 22 Zentimeter.

Umfang Halbkreis

Die obigen Ausführungen beziehen sich jeweils auf einen vollständigen Kreis. Ebenso gut können Sie aber auch den Umfang von einen Halbkreis berechnen. Dieser ist durch den sogenannten Kreisbogen (entspricht der halben Kreislinie) und dem Durchmesser definiert, welcher die Grundlinie bildet.

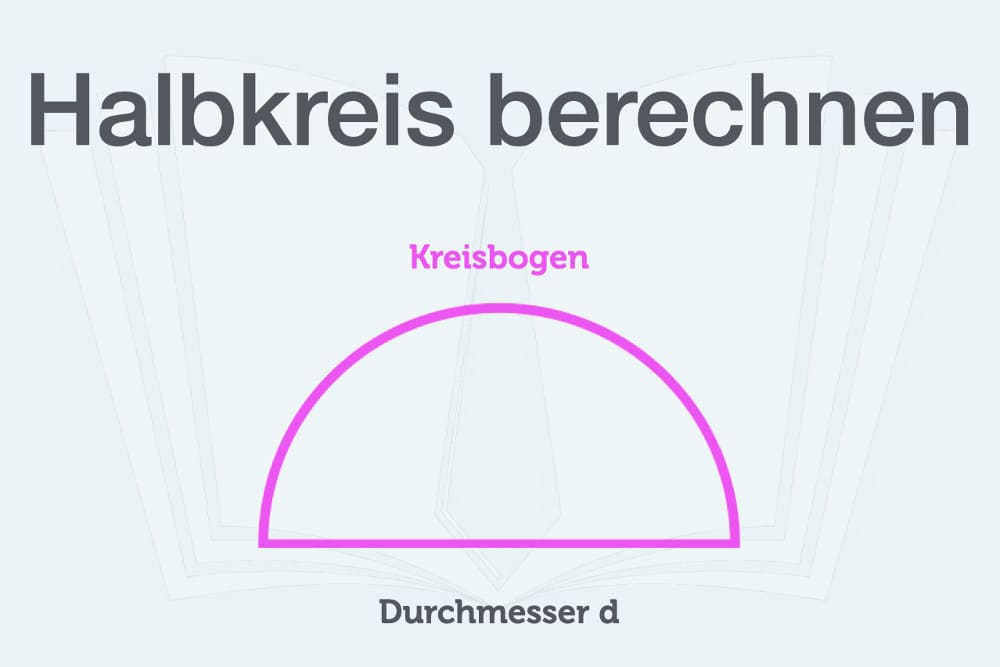
Zur Berechnung des Kreisbogens können Sie die obige Formel für den Kreisumfang heranziehen und anschießend durch zwei teilen. Als Formel ausgedrückt:

u (Halbkreis) = ½ ∙ u (gesamter Kreis) = ½ ∙ 𝜋 ∙ d

Beispiel Berechnung Halbkreis

Sie haben einen Halbkreis mit einem Durchmesser von 6 Zentimetern. Sie rechnen folgendermaßen:

u = ½ ∙ 3,14 ∙ 6 cm = 9,42 cm.

Um nun den ganzen Umfang des Halbkreises zu erhalten, müssen Sie den Umfang des Kreisbogens mit dem Durchmesser addieren, also:

u = u + d = 9,42 cm + 6 cm = 15,42 cm

Tangente, Passante und Sekante

Um den Umfang eines Kreises berechnen zu können, reichen obige Formeln. Die nachfolgenden Erläuterungen dienen zudem als Ergänzung, da sie bei Aufgaben der Kreisberechnung vorkommen können.

Zum Schulstoff der Mathematik in der 7. Klasse gehören geometrische Ortslinien. Ein Kreis und eine Gerade können auf drei verschiedene Arten zueinander angeordnet sein. Die Gerade trägt je nach Lage am Kreis unterschiedliche Bezeichnungen:

• Tangente
  Diese Form der Geraden berührt den Kreis an exakt einem Punkt. Damit ist der Abstand des Mittelpunkts zur Geraden mit dem Radius identisch.
• Passante
  Am Kreis vorbei geht die Passante. Bei dieser Geraden ist der Abstand des Kreismittelpunkts größer als der Kreisradius.
• Sekante
  Eine Gerade, welche den Kreis an zwei Stellen durchtrennt, nennt sich Sekante. Ihr Abstand zum Mittelpunkt ist geringer als der Kreisradius. Verläuft die Sekante direkt durch den Mittelpunkt, heißt sie Zentrale.

Was andere Leser dazu gelesen haben

• Flächeninhalt Dreieck: Berechnung + Beispiele
• Römische Zahlen übersetzen: Regeln, Liste, Tabelle
• Primzahlen erkennen: Definition, Liste + Primfaktorzerlegung
• Dreisatz berechnen: Erklärung, Formel + Aufgaben
• Periodensystem: Erklärung zu Aufbau, Ordnungszahl + PDF
• Binomische Formeln auflösen: Erklärung, Übungen + Beispiele