Einfach erklärt: Was ist das Monty-Hall-Dilemma?
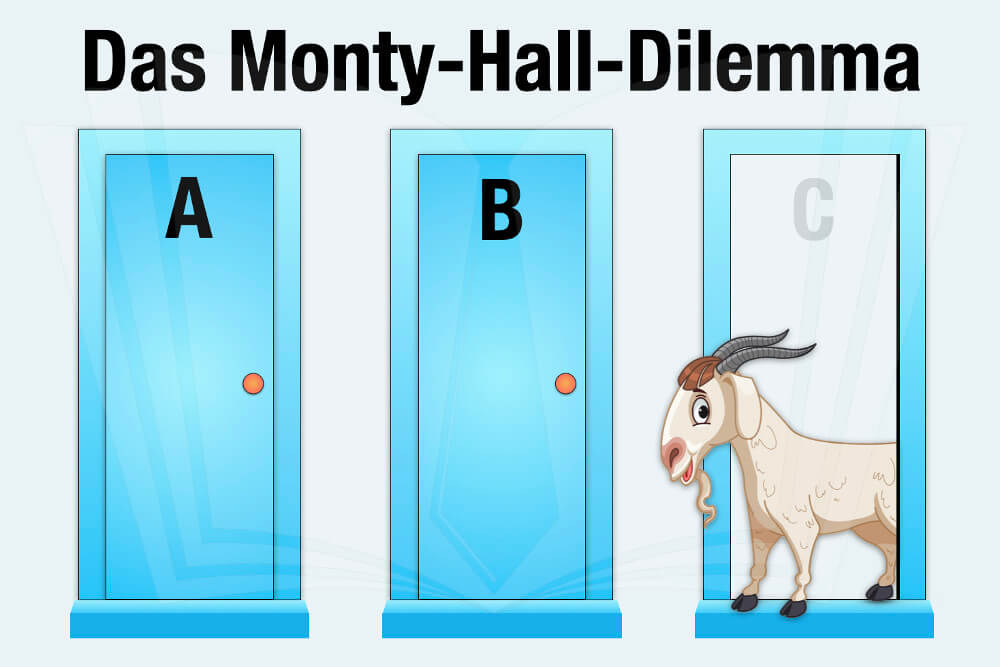
Das Monty-Hall-Dilemma (auch: Ziegenproblem oder Drei-Türen-Dilemma) stammt ursprünglich von der TV-Show „Let’s make a deal“ (in Deutschland: „Geh aufs Ganze“). Dabei hat ein Kandidat die Wahl zwischen drei Optionen oder drei verschlossenen Türen. Hinter einer Tür verbirgt sich ein teures Auto, das der oder die Kandidatin gewinnen kann. Hinter den beiden anderen Türen befinden sich Nieten beziehungsweise Ziegen — daher der Name „Ziegenproblem“ (Der Moderator von „Let’s make a deal“ hieß Monty Hall).
Bei dem Monty Hall Problem kann sich der Spieler zunächst für eine Tür entscheiden. Daraufhin öffnet der Moderator eine der anderen beiden Türen, hinter der sich eine Ziege verbirgt. Es bleiben nun noch zwei Türen übrig: Hinter einer steht das Auto, hinter der anderen eine weitere Ziege. Der Kandidat darf daher nochmal wählen: Bleibt er bei der ersten Entscheidung oder wechselt er und setzt auf die andere Tür?
Stehen die Gewinnchancen wirklich Fifty-Fifty?
Die meisten Menschen denken: Der Moderator will sie nur verunsichern. Die Chancen stehen jetzt genau Fifty-Fifty – egal, ob sie wechseln oder nicht… Falsch! Mathematiker wissen es besser: Sie sollten sich umentscheiden und die Tür wechseln! Damit steigt die Wahrscheinlichkeit, dass Sie das schicke Auto gewinnen auf rund 67 Prozent.
Wechseln oder nicht wechseln: Selbst die seinerzeit „intelligenteste Frau der Welt“, Marilyn vos Savant, riet in der Zeitschrift „Parade“ und in ihrer Kolumne „Ask Marylin“ ganz klar: „Wechseln Sie. Sie verdoppeln damit Ihre Chance zu gewinnen!“ Mit der Empfehlung löste Marilyn vos Savant zwar eine Flut von empörten Leserbriefen aus. Aber sie hatte Recht!
Das Ziegenproblem: Unsere Intuition trügt
Die meisten Menschen wollen das nicht glauben – ihr Bauchgefühl sagt ihnen etwas anderes. Es sind zu diesem Zeitpunkt nur noch zwei verschlossene Türen – eine gewinnt, eine verliert. Es sollte also keine Rolle spielen, ob der Kandidat seine Entscheidung ändert. Bleiben oder Wechseln? Die Gewinnchance liegt intuitiv bei jeweils 50 Prozent…
Stimmt nicht! Auch wenn Ihnen die Intuition etwas anderes sagt – der Schein trügt. Per Mathematik und in Computersimulationen lässt sich beweisen, dass die Lösung des Ziegenproblems tatsächlich darin besteht, von seiner ursprünglichen Wahl abzuweichen. Warum?
Ziegenproblem Lösung: So lösen Sie das Monty-Hall-Dilemma
Der entscheidende Schritt zur Ziegenproblem Lösung ist, die Wahrscheinlichkeit nicht erst dann zu berechnen, wenn der Kandidat zum zweiten Mal wählen darf – also nachdem der Moderator eine Tür mit Ziege geöffnet hat. Bedeutet: Um das Monty-Hall-Dilemma zu lösen, müssen Sie den gesamten Spielverlauf in die Berechnung einbeziehen.
Die folgende Tabelle gibt einen guten Überblick über insgesamt 9 mögliche Spielabläufe. Alle diese Varianten sind gleich wahrscheinlich: Das Auto wird jedes Mal zufällig hinter einer der Türen versteckt und der oder die Kandidatin wählt ebenso zufällig eine der Türen aus, weil außer dem Moderator niemand weiß, hinter welcher Tür das Auto steckt…
Monty-Hall-Dilemma Simulation
| Auto hinter Tür= | Erste Türwahl= | Bleiben | Wechseln |
| 1 | 1 | 🚘 | 🐐 |
| 1 | 2 | 🐐 | 🚘 |
| 1 | 3 | 🐐 | 🚘 |
| 2 | 1 | 🐐 | 🚘 |
| 2 | 2 | 🚘 | 🐐 |
| 2 | 3 | 🐐 | 🚘 |
| 3 | 1 | 🐐 | 🚘 |
| 3 | 2 | 🐐 | 🚘 |
| 3 | 3 | 🚘 | 🐐 |
| Gewinne: 3 von 9 = 1/3 |
Gewinne: 6 von 9 = 2/3 |
Lösung einfach erklärt
Beim Monty-Hall-Dilemma beziehungsweise Ziegenproblem führt die Strategie, auf der ursprünglich Wahl zu beharren, nur dann zu einem Gewinn und Erfolg, wenn die erste Wahl tatsächlich richtig war. Das ist aber nur in drei von neun möglichen Spielverläufen der Fall. Damit beträgt die Wahrscheinlichkeit, mit der Strategie ein Auto zu gewinnen, gerademal 3/9tel – umgerechnet: 33,3 Prozent.
Wer sich dagegen jedes Mal umentscheidet, sobald er oder sie die Möglichkeit dazu bekommt, erzielt in sechs von neun Fällen den Hauptgewinn. Dabei ist es völlig unerheblich, welche Tür der Moderator öffnet – er zeigt sowieso jedes Mal nur eine Tür mit einer Ziege dahinter. Damit liegt die Wahrscheinlichkeit, das Ratespiel zu gewinnen, bei einem Wechsel bei 6/9tel – also 66,7 Prozent.
Auch mit einer Wechselstrategie und Gewinnwahrscheinlichkeit von zwei Drittel gibt es natürlich noch keine Garantie auf den Erfolg. Sie können damit auch weiterhin daneben liegen – nur liegt die Wahrscheinlichkeit, richtig zu liegen, bei einer zweiten Wahl gut doppelt so hoch als wenn Sie bei Ihrer ersten Wahl bleiben.
Was andere dazu gelesen haben
