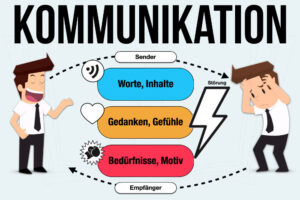
Übersicht: 14 Kriterien bei der Jobauswahl

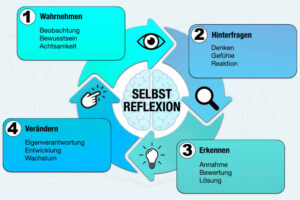
Bei der Jobauswahl geht es immer um individuelle Prioritäten, persönliche Erwartungen und Ziele. Die erste Voraussetzung für eine erfolgreiche Jobauswahl ist deshalb eine gründliche und ehrliche Selbstreflexion.

In unserer Übersicht zeigen wir 14 Kriterien für die Jobauswahl, mit denen Sie den für sich passenden Traumjob finden können:

🎯 Sicherheit

Es gibt keine 100-prozentige Jobsicherheit, doch sollten Sie sich nicht von Anfang an Sorgen um Ihren Arbeitsplatz machen müssen. Ein potenzieller Arbeitgeber sollte deshalb in einer wirtschaftlichen stabilen Lage sein. Nur so können Sie langfristig planen – nicht nur beruflich, sondern auch privat, weil Sie größere finanzielle Sicherheit genießen.

🎯 Aufgabenfeld

Ein wichtiges Kriterium für die Jobauswahl ist das konkrete Aufgabenfeld und die Tätigkeitsbeschreibung. Anders ausgedrückt: Was genau machen Sie in der Position? Aufgaben müssen zu Ihren Stärken und Fähigkeiten passen, vor allem aber auch spannend und herausfordernd sein. Sonst werden Sie bereits nach kurzer Zeit unzufrieden im Job.

🎯 Arbeitsatmosphäre

In Umfragen werden die Arbeitsatmosphäre und das Betriebsklima regelmäßig zum wichtigsten Punkt bei der Jobauswahl und der späteren Zufriedenheit genannt. Schließlich verbringen Sie täglich acht Stunden am Arbeitsplatz mit den Kollegen und Führungskräften. Wenn die Chemie nicht stimmt, ist Frust garantiert. Es braucht Wertschätzung, Anerkennung und gegenseitigen Respekt.

🎯 Aufstiegschancen

Wollen Sie auf der Karriereleiter noch weiter nach oben? Dann müssen Job und Arbeitgeber die entsprechenden Möglichkeiten dazu bieten. Nicht jede Position wird zum Sprungbrett, manchmal ist es eher eine Sackgasse. Informieren Sie sich bereits vor der Jobauswahl, wie die Aufstiegschancen stehen – oder ob die Chancen schlecht sind und Sie Ihre Karrierepläne woanders verwirklichen sollten.

🎯 Weiterbildungsmöglichkeiten

Zur beruflichen Entwicklung gehören auch Weiterbildungen oder Angebote für Fortbildungen. Wenn Sie Ihre Fähigkeiten ausbauen oder Wissen vertiefen wollen, sollte der Arbeitgeber Sie bei dem Vorhaben unterstützen. Manche Unternehmen fördern eigene Mitarbeiter aktiv und umfangreich, andere halten sich aus dem Thema komplett raus.

🎯 Eigenverantwortung

Viele Arbeitnehmer wünschen sich Eigenverantwortung und selbstständiges Entscheiden im Job. Nicht jeder kommt mit einem Mikromanager klar, der gerne alles kontrolliert und bei jeder Aufgabe über die Schulter guckt.

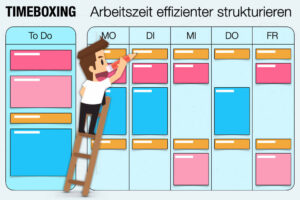
🎯 Flexible Arbeitszeiten

In der heutigen Zeit ein besonders wichtiger Faktor. Wollen Sie in einem klassischen 9-to-5-Job arbeiten oder wünschen Sie sich flexiblere Arbeitszeiten? Gerade jüngere Generationen wünschen sich mehr Gestaltungsspielraum bei der Arbeit. Das gilt gleichermaßen für den Arbeitsort. Regelungen zum Homeoffice oder Modelle zum mobilen Arbeiten können Kriterien für die Jobauswahl sein.

🎯 Selbstverwirklichung

Der Job sollte mehr sein als nur Broterwerb. Er ist ein Mittel zur Selbstverwirklichung. Sie können die Arbeit mitgestalten, Ihre Ideen einbringen, eigene Projekte entwickeln und umsetzen. Ein solcher Arbeitsplatz wird als erfüllend und sinnstiftend empfunden, macht langfristig glücklich und erfolgreich.

🎯 Zusatzleistungen

Zusatzleistungen sind Extras, die ein Arbeitgeber seinen Mitarbeitern bietet. Das können monetäre Incentives sein, aber auch nicht-monetäre Leistungen können einen Unterschied machen. Bei der Jobauswahl lohnt es sich deshalb, neben den reinen Gehaltszahlen auf andere Benefits zu achten.

🎯 Unternehmenskultur

Werte, Kommunikation, Hierarchien und der Umgang untereinander – die Unternehmenskultur sollte zu Ihren Vorstellungen passen. Sie müssen sich mit Ihrem Arbeitgeber identifizieren können, um motiviert zu arbeiten und Unternehmensziele zu verfolgen.

🎯 Führungsverhalten

Mitarbeiter kommen wegen des Jobs, bleiben wegen der Aufgabe und gehen wegen des Chefs… Achten Sie auf das Verhalten von Führungskräften und machen Sie sich möglichst frühzeitig ein Bild vom Führungsstil. Das kann bei einem Probearbeiten sein, aber auch im Vorstellungsgespräch oder während der anfänglichen Probezeit. Wählen Sie einen Job, bei dem Führungsverhalten mit Ihren Erwartungen und Ihrer Arbeitsweise zusammenpassen.

🎯 Employer Branding

Im Internet, über Bewertungsportale oder über Kontakte zu Mitarbeitern können Sie viel über das Employer Branding erfahren. Achten Sie dabei nicht nur auf die Werbung von Unternehmen selbst, sondern auch andere Informationsquellen. So erkennen Sie, ob beispielsweise Work-Life-Balance nur auf die Fahnen geschrieben oder tatsächlich umgesetzt wird.

🎯 Vereinbarkeit von Familie und Beruf

Für berufstätige Eltern ist die Vereinbarkeit von Familie und Beruf ein entscheidendes Kriterium der Jobauswahl. Längst nicht jeder Arbeitgeber geht dabei auf die Bedürfnisse der Arbeitnehmer ein. Wie wird das Thema Elternzeit behandelt? Wie flexibel können Sie sein, wenn Sie kurzfristig Ihr Kind betreuen müssen? Solche Fragen sollten im Vorfeld der Jobauswahl geklärt werden.

🎯 Gehalt

Das Gehalt ist natürlich ein zentraler Faktor und ohne eine unfaire Bezahlung kann ein ansonsten attraktives Jobangebot ruinieren. Trotzdem ist es nicht der wichtigste Faktor und sollte nicht das einzige Kriterium für die Jobauswahl sein. Ein guter Verdienst tröstet auf Dauer nicht über einen Job hinweg, der Ihnen nicht gefällt und an dem die Rahmenbedingungen nicht stimmen.

Endlich das Gehalt, das Sie wirklich verdienen!

Fühlen Sie sich unterbezahlt? Dann ist das IHRE Chance auf eine satte Gehaltserhöhung – schon hunderte zufriedene Teilnehmer empfehlen den Kurs weiter: Die erprobte und einfache Anleitung für eine erfolgreiche Gehaltsverhandlung. Mit diesen Strategien überzeugen Sie den Chef mit Leichtigkeit:

Hier geht’s zu Ihrem Wunschgehalt

Optimal-Stopping-Theorie: Zeitpunkt für die Jobauswahl

Sie sind erfolgreich auf Jobsuche, haben viele Vorstellungsgespräche und stehen vor der Jobauswahl. Wann genau treffen Sie Ihre Entscheidung? Darauf gibt es tatsächlich eine mathematische Antwort in der sogenannten Optimal-Stopping-Theorie. Die Grundlage: Nach jedem Gespräch müssen Sie sofort entscheiden: Job annehmen oder ablehnen? Es gibt kein Zurück.

Laut Theorie liegt der Optimal-Stopping-Point bei 37 Prozent. Sie lehnen 37 Prozent der Jobangebote ab – und wählen den nächsten Job, der das bisher beste Angebot übertrifft. Angenommen Sie haben 16 Gespräche vereinbart, müssten Sie somit (gerundet) die ersten 6 Jobs ablehnen, sich einprägen, was davon am besten war und ab dem siebten Interview akzeptieren, wenn ein noch besserer Job kommt.

Perfekter Zeitpunkt funktioniert nur in der Theorie

Leider funktioniert dieser perfekte Zeitpunkt nur in der Theorie. In der Praxis würden Sie natürlich alle Vorstellungsgespräche durchlaufen und erst am Schluss die Jobauswahl treffen – und müssen sich nicht gleich im Anschluss an jedes Gespräch festlegen. Auch ist es keine Garantie für die beste Wahl. Schließlich könnte der Traumjob schon in den ersten (abgelehnten) Stellen liegen. Trotzdem zeigt das Gedankenspiel, wie wichtig es ist, die Jobauswahl gründlich abzuwägen.

Was andere dazu gelesen haben